Introduction

  We propose to extend the ontology of logical AI to include approximate objects, approximate predicates and approximate theories. Besides the ontology we discuss relations among different approximations to the same or similar phenomena.

The article will be as precise as we can make it. We apply Aristotle's remark to the approximate theories themselves. The article treats three topics.

Approximate objects

These are not fully defined, e.g. the wishes of the United States. They may be approximations to more fully defined objects or they may be intrinsically approximate (partial). We give lots of examples, because we don't have precise definitions.

Approximate theories

These often involve necessary conditions and sufficient conditions but lack conditions that are both necessary and sufficient.

Relations among approximate entities

It is often necessary to relate approximate entities, e.g. objects or theories, to less approximate entities, e.g. to relate a theory in which one block is just on another to a theory in which a block may be in various positions on another.

In principle, AI theories, e.g. the original proposals for situation calculus, have allowed for rich entities which could not be fully defined. However, almost all theories used in existing AI research has not taken advantage of this generality. Logical AI theories have resembled formal scientific theories in treating well-defined objects in well-defined domains. Human-level AI will require reasoning about approximate entities.

Approximate predicates can't have complete if-and-only-if definitions and usually don't even have definite extensions. Some approximate concepts can be refined by learning more and some by defining more and some by both, but it isn't possible in general to make them well-defined. Approximate concepts are essential for representing common sense knowledge and doing common sense reasoning. In this article, assertions involving approximate concepts are represented in mathematical logic.

A sentence involving an approximate concept may have a definite truth value even if the concept is ill-defined. It is definite that Mount Everest was climbed in 1953 even though exactly what rock and ice is included in that mountain is ill-defined. We discuss the extent to which we can build solid intellectual structures on such swampy conceptual foundations.

Quantitative approximation is one kind considered--but not the most interesting or the kind that requires logical innovation. Fuzzy logic involves a semi-quantitative approximation, although there are extensions as mentioned in [Zad99].

For AI purposes, the key problem is relating different approximate theories of the same domain. For this we use mathematical logic fortified with contexts as objects. Further innovations in logic may be required to treat approximate concepts as flexibly in logic as people do in thought and language.

Looked at in sufficient detail, all concepts are approximate, but some are precise enough for a given purpose. McCarthy's weight measured by a scales is precise enough for medical advice, and can be regarded as exact in a theory of medical advice. On the other hand, McCarthy's purposes are approximate enough so that almost any discussion of them is likely to bump against its imprecision and ambiguity. Many concepts used in common sense reasoning are imprecise. Here are some questions and issues that arise.

1. What rocks and ice constitute Mount Everest?
2. When can it be said that one block is on another block, so that
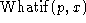   may be asserted?

   Let there be an axiomatic theory in situation calculus in which it can be shown that a sequence of actions will have a certain result. Now suppose that a physical robot is to observe that one block is or is not on another and determine the actions to achieve a goal using situation calculus. It is important that the meanings of 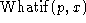used in solving the problem theoretically and that used by the robot correspond well enough so that carrying out a plan physically has the desired effect. How well must they correspond?

3. What are the logical relations between different logical specifications of an approximate object?
4. What are the relations between different approximate logical theories of a domain?

We claim

1. The common sense informatic situation often involves concepts which cannot be made precise. This is a question of the information available and not about computation power. It is not a specifically human limitation and will apply to computers of any possible power. This is not a claim about physics; it may be that a discoverable set of physical laws will account for all phenomena. It is rather a question of the information actually available about particular situations by people or robots with limited opportunities to observe and compute.
2. Much pedantry in science and in philosophy results from demanding if-and-only-if definitions when this is inappropriate.
3. None of the above objects and predicates admits a completely precise if-and-only-if definition.
4. Formalized scientific theories, e.g. celestial mechanics and the blocks world often have precise concepts. They are necessary tools for understanding and computation. However, they are imbedded in common sense knowledge about how to apply them in world of imprecise concepts. Moreover, the concepts are precise only within the theory. Most AI theories have also had this character.
5. Almost all concepts are approximate in the full common sense informatic situation. However, many are precise, i.e. have if-and-only-if definitions in particular contexts.
6. The human reasoning processes involving common sense knowledge correspond only partly to the mathematical and logical reasoning processes that humans have used so successfully within scientific and mathematical theories.
7. Nevertheless, mathematical logic is an appropriate tool for representing this knowledge and carrying out this reasoning in intelligent machines. The use of logic will certainly require adaptations, and the logic itself may require modifications.
8. Key tools for common sense reasoning by machines will be approximate concepts and approximate theories. These are in addition to formalized non-monotonic reasoning and formal theories of context.
9. The most important notion of approximation for common sense reasoning is not the familiar numerical approximation but a new kind of logical approximation appropriate for common sense reasoning. These mostly differ from the approximations of fuzzy logic.

In the subsequent sections of this article, tools will be proposed for reasoning with approximate concepts.

The article treats successively approximate objects, approximate theories, and formalisms for describing how one object or theory approximates another.