The usual AI situation calculus blocks world has a propositional
fluent ![]() asserting that block x is on block y. We
can assert
asserting that block x is on block y. We
can assert ![]() about some situation s
and have the action
about some situation s
and have the action ![]() that moves block x on top of
block y.
that moves block x on top of
block y.
Suppose this formalism is being used by a robot acting in the real
world. The concepts denoted by ![]() , etc. are then approximate
concepts, and the theory is an approximate theory. Our goal is to
relate this approximate theory to the real world. Similar
considerations would apply if we were relating it to a more
comprehensive but still approximate theory.
, etc. are then approximate
concepts, and the theory is an approximate theory. Our goal is to
relate this approximate theory to the real world. Similar
considerations would apply if we were relating it to a more
comprehensive but still approximate theory.
We use formalized contexts as in [McC93b] and [MB97].
and let 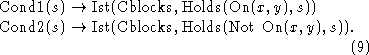 be a
blocks world context with a language allowing On(x,y), etc.
be a
blocks world context with a language allowing On(x,y), etc.
![]() is approximate
in at least the following respects.
is approximate
in at least the following respects.
![]() and
and ![]() are respectively conditions
in the outer context on the situation s that x shall be on y
and x shall not be on y in the context
are respectively conditions
in the outer context on the situation s that x shall be on y
and x shall not be on y in the context 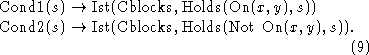 . These
need not be the negations of each other, so it can happen that it
isn't justified to say either that x is on y or that it isn't.
. These
need not be the negations of each other, so it can happen that it
isn't justified to say either that x is on y or that it isn't.
![]() and
and ![]() need not be mutually
exclusive. In that case the theory associated with
need not be mutually
exclusive. In that case the theory associated with
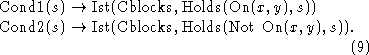 would be inconsistent. However, unless there are
strong lifting rules the inconsistency within
would be inconsistent. However, unless there are
strong lifting rules the inconsistency within
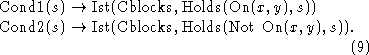 cannot infect the rest of the reasoning.
cannot infect the rest of the reasoning.
Notice that the theory in the context 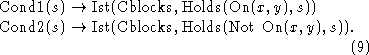 approximates a theory
in which blocks can be in different orientations on each other or in
the air or on the table in quite different sense than numerical
approximation.
approximates a theory
in which blocks can be in different orientations on each other or in
the air or on the table in quite different sense than numerical
approximation.