The theory of conditional expressions corresponds to analysis by cases in mathematics and is only a mild generalization of propositional calculus.
We start by considering expressions called generalized Boolean forms (gbf) formed as follows:
1. Variables are divided into propositional variables p, q, r, etc. and general variables x, y, z, etc.
2. We shall write ![]() for
for ![]() is called an elementary
conditional form (ecf) of which p, x, and y are called the
premiss, conclusion and the alternative,
respectively.
is called an elementary
conditional form (ecf) of which p, x, and y are called the
premiss, conclusion and the alternative,
respectively.![]()
3. A variable is a gbf, and if it is a propositional variable it is called a propositional form (pf).
4. If ![]() is a pf and
is a pf and ![]() and
and ![]() are gbfs, then
are gbfs, then ![]() is a gbf. If, in addition,
is a gbf. If, in addition, ![]() and
and ![]() are
pfs, so is
are
pfs, so is ![]()
The value of a gbf ![]() for given values (T, F or undefined) of the
propositional variables will be T or F in case
for given values (T, F or undefined) of the
propositional variables will be T or F in case ![]() is a pf or a
general variable otherwise. This value is determined for a gbf
is a pf or a
general variable otherwise. This value is determined for a gbf ![]() according to the table
according to the table

We shall say that two gbfs are strongly equivalent if they have the same value for all values of the propositional variables in them including the case of undefined propositional variables. They are weakly equivalent if they have the same values for all values of the propositional variables when these are restricted to F and T.
The equivalence of gbfs can be tested by a method of truth tables
identical to that of propositional calculus. The table for ![]() and
and ![]() is given on the foregoing page.
is given on the foregoing page.
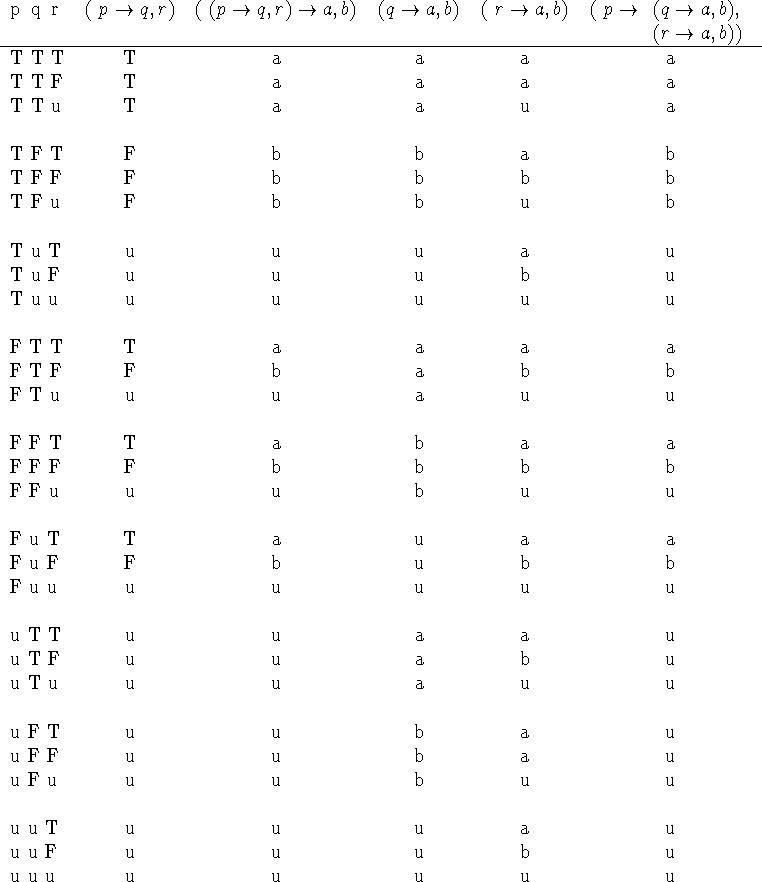
According to the table, ![]() and
and
![]() are strongly
equivalent.
are strongly
equivalent.
For weak equivalence the u case can be left out of the table.
Consider the table,
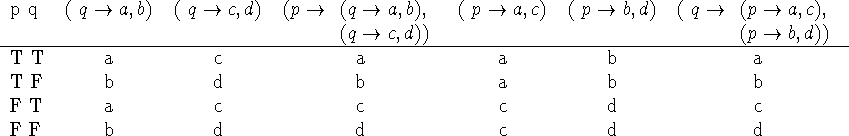
which proves that ![]() and
and ![]() are weakly equivalent. They are also strongly equivalent. We shall write
are weakly equivalent. They are also strongly equivalent. We shall write ![]() and
and ![]() for the relations of strong and weak equivalence.
for the relations of strong and weak equivalence.
There are two rules whereby an equivalence can be used to generate other equivalences.
1. If ![]() and
and ![]() is the result of
substituting any gbf for any variable in
is the result of
substituting any gbf for any variable in ![]() then
then ![]() This is called the rule of substitution.
This is called the rule of substitution.
2. If ![]() and
and ![]() is subexpression of
is subexpression of ![]() and
and
![]() is the result of replacing an occurrence of
is the result of replacing an occurrence of ![]() in
in ![]() by an occurrence of
by an occurrence of ![]() , then
, then ![]() This is
called the rule of replacement.
This is
called the rule of replacement.
These rules are applicable to either strong or weak equivalence and in fact to much more general situations.
Weak equivalence corresponds more closely to equivalence of truth functions in propositional calculus than does strong equivalence.
Consider the equations
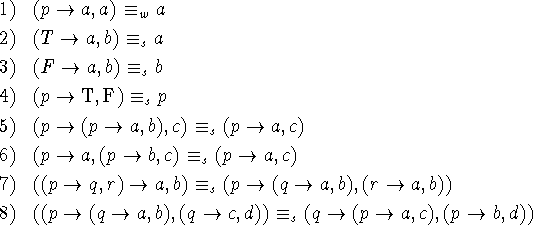
All are strong equivalence except the first, and all can be proved by truth tables.
These eight equations can be used as axioms to transform any gbf into any weakly equivalent one using substitution and replacement.
In fact, they can be used to transform any gbf into a canonical
form. This canonical form is the following. Let ![]() be the
variables of the gbf a taken in an arbitrary order. Then a can be
transformed into the form
be the
variables of the gbf a taken in an arbitrary order. Then a can be
transformed into the form
![]()
where each ![]() has the form
has the form
![]()
and in general for each k = 1,...,n-1
![]()
and each ![]() is a truth value or a general variable.
is a truth value or a general variable.
For example, the canonical form of
![]()
with the variables taken in the order r, q, p is
![]()
In this canonical form, the 2 ![]() cases of the truth or falsity of
cases of the truth or falsity of ![]() are explicitly exhibited.
are explicitly exhibited.
An expression may be transformed into canonical form as follows:
1) Axiom 7 is used repeatedly until in every subexpression the ![]() in
in ![]() consists of a single propositional
variable.
consists of a single propositional
variable.
2) The variable ![]() is moved to the front by repeated application of
axiom 8. There are three cases:
is moved to the front by repeated application of
axiom 8. There are three cases: ![]() to which axiom 8 is directly applicable;
to which axiom 8 is directly applicable;
![]() where axiom 8 becomes
applicable after axiom 1 is used to make it
where axiom 8 becomes
applicable after axiom 1 is used to make it ![]() the case
the case ![]() which is handled in a manner similar to that
of case 2.
which is handled in a manner similar to that
of case 2.
Once the main expression has the form ![]() we move any
we move any ![]() 's which occur in
's which occur in ![]() and
and ![]() to the front and
eliminate them using axioms 5 and 6. We then bring
to the front and
eliminate them using axioms 5 and 6. We then bring ![]() to the front of
to the front of ![]() and
and ![]() using axiom 1 if necessary to guarantee at least one occurrence
of
using axiom 1 if necessary to guarantee at least one occurrence
of ![]() in each of
in each of ![]() and
and ![]() . The process is continued until the
canonical form is achieved.
. The process is continued until the
canonical form is achieved.
There is also a canonical form for strong equivalence. Any gbf a is
strongly equivalent to one of the form ![]() ,
where
,
where ![]() and
and ![]() do not contain
do not contain ![]() and are themselves in
canonical form. However, the variable
and are themselves in
canonical form. However, the variable ![]() may not be chosen
arbitrarily but must be an inevitable propositional variable of
the original gbf and can be chosen to be any inevitable variable. An
inevitable variable of a gbf
may not be chosen
arbitrarily but must be an inevitable propositional variable of
the original gbf and can be chosen to be any inevitable variable. An
inevitable variable of a gbf ![]() is defined to
be either the first propositional variable or else an inevitable
variable of both
is defined to
be either the first propositional variable or else an inevitable
variable of both ![]() and
and ![]() . Thus p and q are the inevitable
variables of
. Thus p and q are the inevitable
variables of
![]()
A gbf a may be put in strong canonical form as follows:
1) Use axiom 7 to get all premisses as propositional variables.
2) Choose any inevitable variable, say ![]() and put a in the form
and put a in the form ![]() by using axiom 8.
by using axiom 8.
3) The next step is to eliminate occurrences of ![]() in
in ![]() and
and
![]() . This can be done by the general rule that in any ecf
occurrences of the premiss in the conclusion can be replaced by T and
occurrences in the alternative by F. However, if we wish to use
substitution and replacement on formulas we need the additional
axioms
. This can be done by the general rule that in any ecf
occurrences of the premiss in the conclusion can be replaced by T and
occurrences in the alternative by F. However, if we wish to use
substitution and replacement on formulas we need the additional
axioms
(9) ![]()
and
(10) ![]()
Suppose there is an occurrence of ![]() in the conclusion; we want to
replace it by T. To do this, we use axioms 9 and 10 to move in a
in the conclusion; we want to
replace it by T. To do this, we use axioms 9 and 10 to move in a ![]() until the objectionable
until the objectionable ![]() occurs as the inner
occurs as the inner ![]() of one of the
forms
of one of the
forms
![]()
or
![]()
In either case, the objectionable ![]() can be removed by axiom 5 or 6, and the
can be removed by axiom 5 or 6, and the
![]() 's that were moved in can be moved out again.
's that were moved in can be moved out again.
Thus we have ![]() with
with ![]() missing from
missing from ![]() and
and ![]()
4) Inevitable variables are then brought to the front of ![]() and
and ![]() and so forth.
and so forth.
Two gbfs are equivalent (weakly or strongly) if and only if they have the same (weak or strong) canonical form. One way this is easy to prove; if two gbfs have the same canonical form they can be transformed into each other via the canonical form. Suppose two gbfs have different weak canonical forms when the variables are taken in the same order. Then values can be chosen for the p's giving different values for the form proving non-equivalence. In the strong case, suppose that two gbfs do not have the same inevitable propositional variables. Let p be inevitable in a but not in b. Then if the other variables are assigned suitable values b will be defined with p undefined. However, a will be undefined since p is inevitable in a which proves non-equivalence. Therefore, strongly equivalent gbfs have the same inevitable variables, so let one of them be put in front of both gbfs. The process is then repeated in the conclusion and alternative etc.
The general conditional form
![]()
can be regarded as having the form
![]()
where u is a special undefined variable and their properties can be derived from those of gbf's.
The relation of functions to conditional forms is given by the distributive law
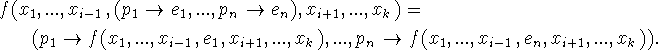
The rule of replacement can be extended in the case of conditional
expressions. Suppose ![]() is an occurrence of a subexpression of an
expression
is an occurrence of a subexpression of an
expression ![]() . We define a certain propositional expression
. We define a certain propositional expression ![]() called the premiss of
called the premiss of ![]() in
in ![]() as follows:
as follows:
1) The premiss of ![]() in
in ![]() is T
is T
2) The premiss of ![]() in
in ![]() where
where ![]() is part of
is part of ![]() is the premiss of
is the premiss of ![]() in
in ![]()
3) If ![]() occurs in
occurs in ![]() and the premiss of
and the premiss of ![]() in
in ![]() is
is ![]() , then the premiss of
, then the premiss of ![]() in
in ![]() is
is ![]()
4) If ![]() occurs in
occurs in ![]() and the premiss of
and the premiss of ![]() in
in ![]() is
is ![]() , then the premiss of
, then the premiss of ![]() in
in ![]() is
is ![]()
The extension of the rule of replacement is that an occurrence
of ![]() in
in ![]() may be replaced by
may be replaced by ![]() if
if ![]() where
where ![]() is the premiss of
is the premiss of ![]() in
in
![]() . Thus in a subcase one needs only prove equivalence under the
premiss of the subcase.
. Thus in a subcase one needs only prove equivalence under the
premiss of the subcase.