In the previous sections on recursive definition of functions the domains and ranges of the basic functions were prescribed and the defined functions had the same domains and ranges.
In this section we shall consider the definition of new sets and the basic functions on them. First we shall consider some operations whereby new sets can be defined.
1. The Cartesian product ![]() of two sets A and B is
the set of all ordered pairs
of two sets A and B is
the set of all ordered pairs ![]() with
with ![]() and
and ![]() . If A and B are finite sets and n(A) and n(B) denote
the numbers of members of A and B respectively then
. If A and B are finite sets and n(A) and n(B) denote
the numbers of members of A and B respectively then ![]() .
.
Associated with the pair of sets (A,B) are two canonical
mappings:
![]() defined by
defined by ![]()
![]() defined by
defined by ![]()
The word ``canonical'' refers to the fact that ![]() and
and
![]() are defined by the sets A and B and do not depend
on knowing anything about the members of A and B.
are defined by the sets A and B and do not depend
on knowing anything about the members of A and B.
The next canonical function ![]() is a function of two variables
is a function of two variables
![]() defined by
defined by
![]()
For some purposes functions of two variables, x from A and y
from B, can be identified with functions of one variable defined on
![]()
2. The direct union ![]() of the sets A and B is
the union of two non-intersecting sets one of which is in 1-1
correspondence with A and the other with B. If A and B are
finite, then
of the sets A and B is
the union of two non-intersecting sets one of which is in 1-1
correspondence with A and the other with B. If A and B are
finite, then ![]() even if A and B
intersect. The elements of
even if A and B
intersect. The elements of ![]() may be written as elements of
A or B subscripted with the set from which they come, i.e.
may be written as elements of
A or B subscripted with the set from which they come, i.e. ![]() or
or ![]()
The canonical mappings associated with the direct union ![]() are
are
![]() defined by
defined by ![]()
![]() defined by
defined by ![]()
![]() defined by
defined by ![]() = T if and only if x comes from A,
= T if and only if x comes from A,
![]() defined by
defined by ![]() = T if and only if x comes from B.
= T if and only if x comes from B.
There are two canonical partial functions ![]() and
and ![]() .
. ![]() is defined only for elements
coming from A and satisfies
is defined only for elements
coming from A and satisfies ![]() Similarly,
Similarly,
![]() satisfies
satisfies ![]()
3. The power set ![]() is the set of all mappings
is the set of all mappings ![]() The canonical mapping
The canonical mapping ![]() is defined by
is defined by
![]()
Canonical mappings. We will not regard the sets ![]() and
and ![]() as the same, but there is a canonical 1-1
mapping between them,
as the same, but there is a canonical 1-1
mapping between them,
![]()
defined by
![]()
We shall write
![]()
to express the fact that these sets are canonically isomorphic.
Other canonical isomorphisms are
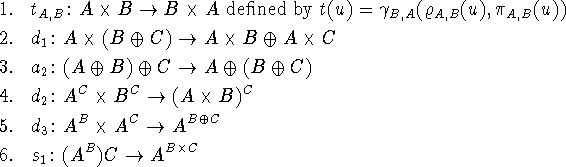
We shall denote the null set (containing no elements) by 0 and the set consisting of the integers from 1 to n by n. We have

Suppose we write the recursive equation
![]()
We can interpret this as defining the set of sequences of elements of A as follows:
1. Interpret ![]() as denoting the null sequence. Then the null sequence
(strictly an image of it) is an element of S.
as denoting the null sequence. Then the null sequence
(strictly an image of it) is an element of S.
2. Since a pair consisting of an element of A and an element of S is an
element of S, a pair ![]() is an element of S. So, then, are
is an element of S. So, then, are
![]()
Thus S consists of all sequences of elements of A including the null sequence.
Suppose we substitute ![]() for S in the right side of
for S in the right side of ![]() . We get
. We get
![]()
If we again substitute for S and expand by the distributive law expressed in equation (2) above we get
![]()
which, if we now denote the set ![]() by 1, becomes
by 1, becomes
![]()
which is another way of writing the set of sequences. We shall denote the set of sequences of elements of A by seq(A).
We can also derive this relation by writing ![]() and solving formally for S, getting S = 1/(1-A) which we
expand in geometric series to get
and solving formally for S, getting S = 1/(1-A) which we
expand in geometric series to get ![]() just as before.
just as before.
Another useful recursive construction is
![]()
Its elements have the forms a or ![]() or
or ![]() or
or ![]() etc. Thus we have the
set of S-expressions on the alphabet A which we may denote by
sexp(A). This set is the subject matter of Reference 7, and the
following paragraph refers to this paper.
etc. Thus we have the
set of S-expressions on the alphabet A which we may denote by
sexp(A). This set is the subject matter of Reference 7, and the
following paragraph refers to this paper.
When sets are formed by this kind of recursive definition, the canonical mappings associated with the direct sum and Cartesian product operations have significance. Consider, for example, sexp(A).
We can define the basic operations of Lisp, i.e. atom, eq, car, cdr and cons by the equations
![]()
![]()
assuming that equality is defined on the space A.
![]()
![]()
![]()
Definition of the set of integers. Let 0 denote the null set as before.
We can define the set of integers I by
![]()
Its elements are then
![]()
which we shall denote by 0,1,2,3 etc. The successor and predecessor functions are then definable in terms of the canonical operations of the defining equation. We have
![]()
![]()