Another idea of Kempe's can be used to strengthen the reduction process, but regarding it as mere control added to the original logic program seems even harder.
The strengthened reduction procedure also removes countries with four neighbors so that the reduced map contains only countries with five or more neighbors. The validity of this reduction depends on the following Kempe proof that if we have colored a partial map and want to add a country with four neighbors, we can always revise the coloring of the partial map to permit coloring the four neighbor country.
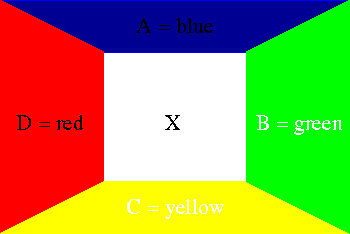
If fewer than four colors have been used to color the neighbors, there is no problem, so suppose that the four neighbors have been colored with four different colors as shown in Figure 2.

Figure 2.
Consider the set S of all countries that can be reached from the blue country A on top of Figure 2 by a path going through only blue and yellow countries. S is called the blue-yellow Kempe component of country A. There are two cases. Either it contains country C or not. If not, we recolor the partial map by reversing blue and yellow on all countries in S. This still leaves the partial map properly colored.
Since S does not contain C, C remains yellow while A has become yellow. This makes blue available to extend the coloring to X.
In the other case, S contains C, i.e, there is a chain of adjacent countries from A to C each of which is colored blue or yellow. Then there cannot be a red-green chain from B to D (by the topology of the plane or sphere), so that a red-green Kempe transformation applied to the red-green Kempe component of D will make D green, leaving red available to color X.
The fact that a blue-yellow path from A to C blocks a red-green path from B to D is where we have used the fact that the map is on a plane or sphere.
This justifies eliminating countries with four neighbors in the
reduction process. If we have colored a partial map and want to add a
country with four neighbors, we can do so, but we may have to modify the
previous coloring by means of a Kempe transformation.![]()
Our improved coloring algorithm then reduces the map by repeatedly dropping countries with four or fewer neighbors, colors the reduced map exhaustively, and then colors the dropped countries in the reverse order using Kempe transformations when necessary.