In order to discuss the role of knowledge in one's ability to achieve goals let us return to the example of the safe. There we had
![]()
which expressed sufficient conditions for the ability of a person to open a safe with a key. Now suppose we have a combination safe with a combination c. Then we may write:
![]()
where we have used the predicate fits2 and the action opens2 to express the distinction between a key fitting a safe and a combination fitting it, and also the distinction between the acts of opening a safe with a key and a combination. In particular, opens2(sf,c) is the act of manipulating the safe in accordance with the combination c. We have left out a sentence of the form has2(p,c,s) for two reasons. In the first place, it is unnecessary: if you manipulate a safe in accordance with its combination it will open; there is no need to have anything. In the second place it is not clear what has2(p,c,s) means. Suppose, for example, that the combination of a particular safe sf is the number 34125, then fits(34125, sf) makes sense and so does the act opens2(sf,34125). (We assume that open(sf,result (p,opens2(sf,34111),s)) would not be true.) But what could has(p,34125,s) mean? Thus, a direct parallel between the rules for opening a safe with a key and opening it with a combination seems impossible.
Nevertheless, we need some way of expressing the fact that one has to know the combination of a safe in order to open it. First we introduce the function combination(sf) and rewrite 2 as
![]()
where csafe(sf) asserts that sf is a combination safe and combination (sf) denotes the combination of sf. (We could not write key(sf) in the other case unless we wished to restrict ourselves to the case of safes with only one key.)
Next we introduce the notion of a feasible strategy for a person. The idea is that a strategy that would achieve a certain goal might not be feasible for a person because he lacks certain knowledge or abilities.
Our first approach is to regard the action
opens2(sf,combination (sf)) as infeasible because p might not
know the combination. Therefore, we introduce a new function
![]() which stands for person p's idea of
the combination of sf in situation s.
which stands for person p's idea of
the combination of sf in situation s.
The action
![]() is regarded as feasible for
p, since p is assumed to know his idea of the combination if this
is defined. However, we leave sentence 3 as it is so we cannot yet
prove
is regarded as feasible for
p, since p is assumed to know his idea of the combination if this
is defined. However, we leave sentence 3 as it is so we cannot yet
prove ![]() .
The assertion that p knows the combination of sf can now be
expressed as
.
The assertion that p knows the combination of sf can now be
expressed as![]()
![]()
and with this, the possibility of opening the safe can be proved.
Another example of this approach is given by the following formalization of getting into conversation with someone by looking up his number in the telephone book and then dialing it.
The strategy for p in the first form is
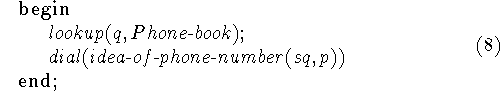
or in the second form

The premisses to write down appear to be
1. ![]()
2. ![]()
3. ![]()
![]()
![]()
4. ![]()
![]()
5. ![]()
6. telephone(Telephone)
7. ![]()
Unfortunately, these premisses are not sufficient to allow one to conclude that
![]()
The trouble is that one cannot show that the fluents at(q,home(q))
and ![]() still apply to the
situation
still apply to the
situation ![]() . To make it come out right we shall revise the
third hypothesis to read:
. To make it come out right we shall revise the
third hypothesis to read:

This works, but the additional hypotheses about what remains unchanged when p looks up a telephone number are quite ad hoc. We shall treat this problem in a later section.
The present approach has a major technical advantage for
which, however, we pay a high price. The advantage is that we
preserve the ability to replace any expression by an equal one in any
expression of our language. Thus if ![]() ,
any true statement of our language that contains 3217580 or
,
any true statement of our language that contains 3217580 or
![]() will remain true if
we replace one by the other.
This desirable property is termed referential transparency.
will remain true if
we replace one by the other.
This desirable property is termed referential transparency.
The price we pay for referential transparency is that we have
to introduce ![]() as a separate ad hoc
entity and cannot use the more natural
as a separate ad hoc
entity and cannot use the more natural ![]() where
where ![]() is some kind of operator applicable to the
concept con. Namely, the sentence
is some kind of operator applicable to the
concept con. Namely, the sentence
![]()
would be supposed to express that p knows
q's phone-number, but ![]() expresses only
that p understands that number. Yet with transparency and the
fact that
expresses only
that p understands that number. Yet with transparency and the
fact that ![]() we could derive the former
statement from the latter.
we could derive the former
statement from the latter.
A further consequence of our approach is that feasibility of
a strategy is a referentially opaque concept since a strategy
containing ![]() is regarded as feasible
while one containing
is regarded as feasible
while one containing ![]() is not, even though these
quantities may be equal in a particular case. Even so, our language
is still referentially transparent since feasibility is a concept of
the metalanguage.
is not, even though these
quantities may be equal in a particular case. Even so, our language
is still referentially transparent since feasibility is a concept of
the metalanguage.
A classical poser for the reader who wants to solve these difficulties to ponder is, `George IV wondered whether the author of the Waverly novels was Walter Scott' and `Walter Scott is the author of the Waverly novels', from which we do not wish to deduce, `George IV wondered whether Walter Scott was Walter Scott'. This example and others are discussed in the first chapter of Church's Introduction to Mathematical Logic (1956).
In the long run it seems that we shall have to use a formalism with referential opacity and formulate precisely the necessary restrictions on replacement of equals by equals; the program must be able to reason about the feasibility of its strategies, and users of natural language handle referential opacity without disaster. In part 5 we give a brief account of the partly successful approach to problems of referential opacity in modal logic.