This is one of the largest and most active areas of philosophic logic. Prior's book Past, Present and Future (1968) is an extremely thorough and lucid account of what has been done in the field. We have already mentioned the four propositional operators F, G, P, H which Prior discusses. He regards these as modal operators; then the alternativeness relation of the semantic theory is simply the time-ordering relation. Various axiomatizations are given, corresponding to deterministic and nondeterministic tenses, ending and nonending times, etc; and the problems of quantification turn up again here with renewed intensity. To attempt a summary of Prior's book is a hopeless task, and we simply urge the reader to consult it. More recently several papers have appeared (see, for instance, Bull 1968) which illustrate the technical sophistication tense-logic has reached, in that full completeness proofs for various axiom systems are now available.
As indicated above, the situation calculus contains a tense-logic (or rather several tense-logics), in that we can define Prior's four operators in our system and by suitable axioms reconstruct various axiomatizations of these four operators (in particular, all the axioms in Bull (1968) can be translated into the situation calculus).
Only one extra nonlogical predicate is necessary to do this: it is a binary predicate of situations called cohistorical, and is intuitively meant to assert of its arguments that one is in the other's future. This is necessary because we want to consider some pairs of situations as being not temporally related at all. We now define F (for instance) thus:
![]()
The other operators are defined analogously.
Of course we have to supply axioms for `cohistorical' and
time: this is not difficult. For instance, consider one of Bull's
axioms, say ![]() , which is better (for us) expressed in the form
, which is better (for us) expressed in the form
![]() . Using the definition, this translates into:
. Using the definition, this translates into:
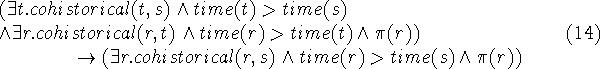
which simplifies (using the transitivity of `>') to
![]()
that is, the transitivity of `cohistorical'. This axiom is precisely
analogous to the S4 axiom
![]() , which corresponded to
transitivity of the alternativeness relation in the modal semantics.
Bull's other axioms translate into conditions on `cohistorical' and
time in a similar way; we shall not bother here with the rather
tedious details.
, which corresponded to
transitivity of the alternativeness relation in the modal semantics.
Bull's other axioms translate into conditions on `cohistorical' and
time in a similar way; we shall not bother here with the rather
tedious details.
Rather more interesting would be axioms relating `shrug' to
`cohistorical' and time; unfortunately we have been unable to think
of any intuitively plausible ones. Thus, if two situations are
epistemic alternatives (that is, ![]() then they may or
may not have the same time value (since we want to allow that p may
not know what the time is), and they may or may not be cohistorical.
then they may or
may not have the same time value (since we want to allow that p may
not know what the time is), and they may or may not be cohistorical.