Nonmonotonic Reasoning from Narratives

 

This section is informal, because we want to discuss what the consequences of a narrative should be before discussing how to make circumscription or some other nonmonotonic formalism do what we want. Here are some kinds of inference we want to be able to make.

Preconditions

An action has only those preconditions that can be inferred from the facts at hand.

Ramifications

Only the effects of an event that can be inferred from the narrative are relevant to the future course of the events mentioned in the narrative.

Presence of objects

The only objects satisfying certain fluents in a situation are those for which it follows from what is stated. Some of the ``it follows'' assertions are inferred nonmonotonically. One child will infer that another child has parents but not that the child has a dog.

Normal effect

An event has its normal effect unless something prevents it.

Occurrences

Only such events occur in a situation or its successors as are asserted or inferred or which don't affect conclusions that might be drawn from their nonoccurrence.

This condition must be formalized very carefully, as is apparent when we elaborate a particular event as a sequence of smaller events. ``How did he buy the Kleenex? He took it off the shelf, put it on the counter, paid the clerk and took it home.'' A narrative that just mentions buying the Kleenex should not allow nonmonotonic reasoning that excludes this particular elaboration. Moreover, if we elaborate in this way, we don't want to exclude subsequent elaboration of component events, e.g. elaborating paying the clerk into offering a bill, taking the change, etc.

Inertia

Events change only those fluents they can be inferred to change. Fluents or fluent valued functions may be declared to be dependent by statements like

 

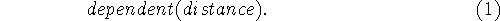
This statement would have the effect of making

change with changes in x and y and have no inertia of its own.

Processes that have started in a situation continue until something changes their course or they terminate as called for in their axiomatizations.

Obstacles

Only such obstacles arise to events having their normal effects as can be inferred.

Actions

Minimize unmotivated actions.

We will very likely use something like the Reiter and Levesque technique of a two stage minimization. (Reiter's Research Excellence lecture and subsequent discussions.) (Advice to use this technique may serve as an example of the declarative expression of heuristics.)