Realizing the Kempe transformation algorithm as control of the Pereira-Porto logic presents a more difficult challenge to the designers of control languages for logic programming. Of course, the postponement part of the algorithm is the same as before; the difficulty comes when it is necessary to color a country with four differently colored neighbors.
The first step is to identify opposite neighbors of the four neighbor
country. This depends not merely on the fact that the map is planar
but on the actual imbedding in the plane. This information has been
discarded when the map is represented as a graph. If the graph is
described by giving for each country a list of its neighbors, the
imbedding information can be including by listing the neighbors in
cyclic order -- clockwise or counterclockwise. Otherwise, it can be
restored in general only with difficulty. Figure 3 shows cases
![]() where
this isn't trivial. Of course, we can modify the algorithm to try
every pair of vertices to see if they are unconnected by a path of
their two colors. The above argument shows that this is guaranteed to
succeeed but presumably at somewhat greater cost than if the cyclic
order is known.
where
this isn't trivial. Of course, we can modify the algorithm to try
every pair of vertices to see if they are unconnected by a path of
their two colors. The above argument shows that this is guaranteed to
succeeed but presumably at somewhat greater cost than if the cyclic
order is known.
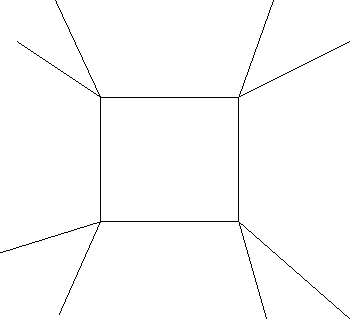
Figure 3.
Looking for a changeable country is a process of search whereby only certain values are allowed for certain variables and goals that become unsatisfied are re-satisfied by changing only certain variables in certain ways. A good control system for logic programs should permit the expression of such strategies.