These notes contain some of the reasoning behind the proposals of [McCarthy, 1987] to introduce contexts as formal objects. The present proposals are incomplete and tentative. In particular the formulas are not what we will eventually want, and I will feel free to use formulas in discussions of different applications that aren't always compatible with each other. [While I dithered, R.V. Guha wrote his dissertation.]
Our object is to introduce contexts as abstract mathematical entities with properties useful in artificial intelligence. Our attitude is therefore a computer science or engineering attitude. If one takes a psychological or philosophical attitude, one can examine the phenomenon of contextual dependence of an utterance or a belief. However, it seems to me unlikely that this study will result in a unique conclusion about what context is. Instead, as is usual in AI, various notions will be found useful.
One major AI goal of this formalization is to allow simple
axioms for common sense phenomena, e.g. axioms for static blocks world
situations, to be lifted to contexts involving fewer
assumptions, e.g. to contexts in which situations change. This is
necessary if the axioms are to be included in general common sense
databases that can be used by any programs needing to know about the
phenomenon covered but which may be concerned with other mattters as
well. Rules for lifting are described in section ![]() and
an example is given.
and
an example is given.
A second goal is to treat the context associated with a particular circumstance, e.g. the context of a conversation in which terms have particular meanings that they wouldn't have in the language in general.
The most ambitious goal is to make AI systems which are never
permanently stuck with the concepts they use at a given time because
they can always transcend the context they are in--if they are
smart enough or are told how to do so. To this end, formulas
![]() are always considered as themselves asserted within
a context, i.e. we have something like
are always considered as themselves asserted within
a context, i.e. we have something like
![]() . The
regress is infinite, but we will show that it is harmless.
. The
regress is infinite, but we will show that it is harmless.
The main formulas are sentences of the form
Contexts are abstract objects. We don't offer a definition, but we will offer some examples. Some contexts will be rich objects, like situations in situation calculus. For example, the context associated with a conversation is rich; we cannot list all the common assumptions of the participants. Thus we don't purport to describe such contexts completely; we only say something about them. On the other hand, the contexts associated with certain microtheories are poor and can be completely described.
Here are some examples.
![]() is the assertion that John McCarthy is at
Stanford University in a context in which it is given that
is the assertion that John McCarthy is at
Stanford University in a context in which it is given that ![]() stands for the author of this paper and that
stands for the author of this paper and that ![]() stands for
Stanford University. The context
stands for
Stanford University. The context ![]() may be one in which the symbol
may be one in which the symbol
![]() is taken in the sense of being regularly at a place, rather than
meaning momentarily at the place. In another context
is taken in the sense of being regularly at a place, rather than
meaning momentarily at the place. In another context ![]() ,
,
![]() may mean physical presence at Stanford at a certain
instant. Programs based on the theory should use the appropriate
meaning automatically.
may mean physical presence at Stanford at a certain
instant. Programs based on the theory should use the appropriate
meaning automatically.
Besides the sentence ![]() , we also want the
term
, we also want the
term ![]() where
where ![]() is a term. For example, we may need
is a term. For example, we may need
![]() , when
, when ![]() is a context that has a time, e.g. a context
usable for making assertions about a particular situation. The
interpretation of
is a context that has a time, e.g. a context
usable for making assertions about a particular situation. The
interpretation of ![]() involves a problem that doesn't
arise with
involves a problem that doesn't
arise with ![]() . Namely, the space in which terms take values
may itself be context dependent. However, many applications will not
require this generality and will allow the domain of terms to be
regarded as fixed.
. Namely, the space in which terms take values
may itself be context dependent. However, many applications will not
require this generality and will allow the domain of terms to be
regarded as fixed.
Here's another example of the value of a term depending on context:
 |
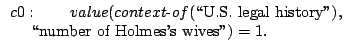 |