
The abstract analytic syntax of the source expressions is given by the table:

which asserts that the expressions comprise constants, variables and binary sums, that the predicates isconst, isvar, and issum enable one to classify each expression and that each sum e has summands s1(e) and s2(e).
The semantics is given by the formula
![]()
where val(e) gives the numerical value of an expression e representing
a constant, ![]() gives the value of the variable e in the state
vector
gives the value of the variable e in the state
vector ![]() and + is some binary operation. (It is natural to regard +
as an operation that resembles addition of real numbers, but our
results do not depend on this).
and + is some binary operation. (It is natural to regard +
as an operation that resembles addition of real numbers, but our
results do not depend on this).
For our present purposes we do not have to give a synthetic syntax for the source language expressions since both the interpreter and the compiler use only the analytic syntax. However, we shall need the following induction principle for expressions:
Suppose ![]() is a predicate applicable to expressions, and suppose that
for all expressions e we have
is a predicate applicable to expressions, and suppose that
for all expressions e we have
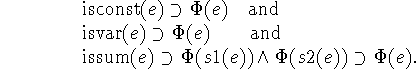
Then we may conclude that ![]() is true for all expressions e.
is true for all expressions e.