AN EVERYWHERE CONTINUOUS NOWHERE DIFFRENTIABLE FUNCTION
John McCarthy, Princeton University
The following is an especially simple example. It is
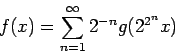
The function ![]() is continuous because it is the uniform limit of
continuous functions. To show that it is not differentiable, take
is continuous because it is the uniform limit of
continuous functions. To show that it is not differentiable, take
![]() , choosing whichever sign makes
, choosing whichever sign makes ![]() and
and
![]() be on the same linear segment of
be on the same linear segment of ![]() . We
have
. We
have
1.
![]() for
for ![]() , since
, since ![]() has
period
has
period
![]()
2.
![]()
3.
![]()
Hence
![]() which goes to infinity with
which goes to infinity with ![]() .
.
The proof that the present example has the required property is simpler than that for any other example the author has seen.
Weierstrass gave the example
![]() for
for ![]() and
and
![]() which is discussed in
Goursat-Hedrick Mathematical Analysis.
which is discussed in
Goursat-Hedrick Mathematical Analysis.
A complete discussion of functions with various singular properties is given in Hobson, Functions of a Real Variable, volume II, Cambridge, 1926.
2006 January note: I was tempted to dig up this 1953 note of mine and put it on my web page by reading The Calculus Gallery by William Dunham. This excellent book includes the first proofs of a number of important theorems, including Weierstrass's proof that his function has the required properties. Dunham's version of Weierstrass's proof is six pages of what Dunham describes as difficult mathematics. Since my proof is 13 lines of what I consider easy math, I decided to copy my old note and discuss it. Dunham recounts that the famous mathematicians Hermite, Poincare and Picard all expressed themselves as repelled by Weierstrass's ``pathological example''. I'm sure that by the time I was born in 1927, such functions were no longer regarded as repellent. My own opinion is that most everywhere continuous functions, in some suitable sense of most, are nowhere differentiable.
Remarks:
1. To prove a function ![]() differentiable at
differentiable at ![]() , one must show that no
matter how
, one must show that no
matter how ![]() goes to zero,
goes to zero,
![]() approaches a limit. To prove
approaches a limit. To prove ![]() non-differentiable at
non-differentiable at ![]() , one need
only find a sequence of values of
, one need
only find a sequence of values of ![]() for which the limit
doesn't exist.
for which the limit
doesn't exist.
2. If ![]() is to be represented as the sum of a series of continuous
functions, it suffices to bound the terms by a suitable positive
terms,
is to be represented as the sum of a series of continuous
functions, it suffices to bound the terms by a suitable positive
terms, ![]() in our case. Then
in our case. Then ![]() is sure to be everywhere
continuous. It doesn't matter how fast the successive terms wiggle.
is sure to be everywhere
continuous. It doesn't matter how fast the successive terms wiggle.
3. In our case, the terms are
![]() . The
. The ![]() grows fast enough to overcome the
grows fast enough to overcome the ![]() damping.
damping.
4. I would expect
![]() to be nowhere differentiable
for most any initial
to be nowhere differentiable
for most any initial ![]() .
.
5. However, the particular ![]() makes the proof easy, because the
periodicity kills the higher terms of the series for
makes the proof easy, because the
periodicity kills the higher terms of the series for ![]() ,
and using
,
and using ![]() for the argument allows the
for the argument allows the ![]() th term to go to
infinity and dominate the earlier terms of the series. It seems lucky
in whatever sense luck exists in mathematics.
th term to go to
infinity and dominate the earlier terms of the series. It seems lucky
in whatever sense luck exists in mathematics.