As the examples of the previous sections have shown, admitting concepts as objects and introducing standard concept functions makes ``quantifying in'' rather easy. However, forming propositions and individual concepts by quantification requires new ideas and additional formalism. We are not very confident of the approach presented here.
We want to continue describing concepts within first order logic with no logical extensions. Therefore, in order to form new concepts by quantification and description, we introduce functions All, Exist, and The such that All(V,P) is (approximately) the proposition that ``for all values of V, P is true'', Exist(V,P) is the corresponding existential proposition, and The(V,P) is the concept of ``the V such that P''.
Since All is to be a function, V and P must be objects in the logic. However, V is semantically a variable in the formation of All(V,P), etc., and we will call such objects inner variables so as to distinguish them from variables in the logic. We will use V, sometimes with subscripts, for a logical variable ranging over inner variables. We also need some constant symbols for inner variables (got that?), and we will use doubled letters, sometimes with subscripts, for these. XX will be used for individual concepts, PP for persons, and QQ for propositions.
The second argument of All and friends is a ``proposition with variables in it'', but remember that these variables are inner variables which are constants in the logic. Got that? We won't introduce a special term for them, but will generally allow concepts to include inner variables. Thus concepts now include inner variables like XX and PP, and concept forming functions like Telephone and Know take as arguments concepts containing internal variables in addition to the usual concepts.
Thus
is a proposition with the inner variable PP in it to the effect that if PP is a child of Mike, then his telephone number is the same as Mike's, and
is the proposition that all Mike's children have the same telephone number as Mike. Existential propositions are formed similarly to universal ones, but the function Exist introduced here should not be confused with the function Exists applied to individual concepts introduced earlier.
In forming individual concepts by the description function The, it doesn't matter whether the object described exists. Thus
is the concept of Mike's only child. ![]() is the proposition that the described child exists. We have
is the proposition that the described child exists. We have
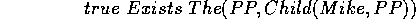
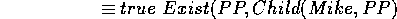
but we may want the equality of the two propositions, i.e.
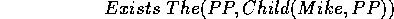
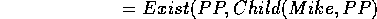
This is part of general problem of when two logically equivalent concepts are to be regarded as the same.
In order to discuss the truth of propositions and the denotation
of descriptions, we introduce possible worlds reluctantly and
with an important difference from the usual treatment.
We need them to give values to the
inner variables, and we can also use them for axiomatizing the
modal operators, knowledge, belief and tense. However, for axiomatizing
quantification, we also need a function ![]() such that
such that
is the possible world that is the same as the world ![]() except that
the inner variable V has the value x instead of the value it
has in
except that
the inner variable V has the value x instead of the value it
has in ![]() . In this respect our possible worlds resemble the state
vectors or environments of computer science more than the
possible worlds of the Kripke treatment of modal logic.
This Cartesian product structure on the space of possible
worlds can also be used to treat counterfactual conditional sentences.
. In this respect our possible worlds resemble the state
vectors or environments of computer science more than the
possible worlds of the Kripke treatment of modal logic.
This Cartesian product structure on the space of possible
worlds can also be used to treat counterfactual conditional sentences.
![]()
Let ![]() be the actual world. Let
be the actual world. Let ![]() mean that the
proposition P is true in the possible world
mean that the
proposition P is true in the possible world ![]() . Then
. Then
Let ![]() mean that X denotes x in
mean that X denotes x in ![]() , and let
, and let
![]() mean the denotation of X in
mean the denotation of X in ![]() when that is
defined.
when that is
defined.
The truth condition for All(V,P) is then given by
Here V ranges over inner variables, P ranges over propositions,
and x ranges over things. There seems to be no harm in making the
domain of x depend on ![]() .
Similarly
.
Similarly
The meaning of The(V,P) is given by
and
We also have the following syntactic rules governing propositions involving quantification:
and
where absent(V,X) means that the variable V is not present in the concept X, and Subst(X,V,Y) is the concept that results from substituting the concept X for the variable V in the concept Y. absent and Subst are characterized by the following axioms:
axioms similar to (92) for other conceptual functions,
axioms similar to (98) for other functions,
and corresponding axioms to (100) for Exist and The.
Along with these comes an axiom corresponding to ![]() -conversion,
-conversion,
The functions absent and Subst play a ``syntactic'' role in describing the rules of reasoning and don't appear in the concepts themselves. It seems likely that this is harmless until we want to form concepts of the laws of reasoning.
We used the Greek letter ![]() for possible worlds, because we
did not want to consider a possible world as a thing and introduce
concepts of possible worlds. Reasoning about reasoning may
require such concepts or else a formulation that doesn't use
possible worlds.
for possible worlds, because we
did not want to consider a possible world as a thing and introduce
concepts of possible worlds. Reasoning about reasoning may
require such concepts or else a formulation that doesn't use
possible worlds.
Martin Davis (in conversation) pointed out the advantages of an alternate treatment avoiding possible worlds in case there is a single domain of individuals each of which has a standard concept. Then we can write