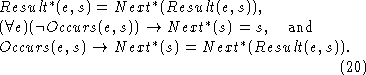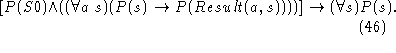Several kinds of mathematical induction seem to be required. For
example, one may want to prove a proposition 
by showing
that it is true for s and is preserved by the events that occur
between s and 
. A related kind of induction is needed to
prove that something is true for all situations arising in the operation
of a buzzer. The simplest case of the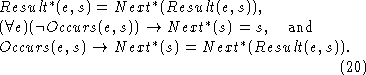 
induction might be to
show that a block unmoved by each of a sequence of events is in the
same position in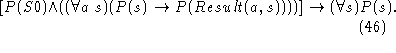 
.
The simplest situation calculus is Reiter's [Rei01]. The formula is
Here are two formulas
(47) is appropriate when 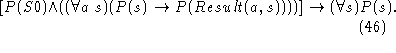is defined.
When 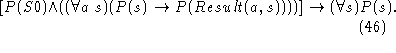is not defined, as in the buzzer case, we can use
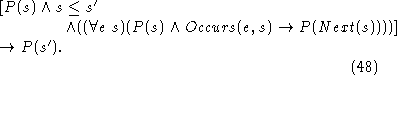to mean that s' is a distant successor of s and have
the axiom.
