We shall assume that there is a map giving for
each variable in the expression a location in the main memory of the
machine loc( ![]() , map) gives this location and we shall assume
, map) gives this location and we shall assume
![]()
as a relation between the state vector ![]() before the compiled program
starts to act and the state vector
before the compiled program
starts to act and the state vector ![]() of the source program.
of the source program.
Now we can write the compiler. It is
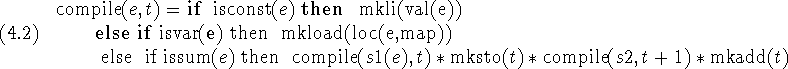
Here t is the number of a register such that all variables are stored in registers numbered less than t, so that registers t and above are available for temporary storage.
Before we can state our definition of correctness of the compiler, we need a notion of partial equality for state vectors
![]()
where ![]() and
and ![]() are state vectors and A is a set of
variables means that
corresponding components of
are state vectors and A is a set of
variables means that
corresponding components of ![]() and
and ![]() are equal except
possibly for values, of variables in A. Symbolically,
are equal except
possibly for values, of variables in A. Symbolically, ![]() . Partial equality satisfies the
following relations:
. Partial equality satisfies the
following relations:
![]()
![]()
![]()
![]()
![]()
In our case we need a specialization of this notation and will use
![]()
and
![]()
and
![]()
The correctness of the compiler is stated in
THEOREM 1. If ![]() and
and ![]() are machine and
source language state vectors respectively such that
are machine and
source language state vectors respectively such that
![]()
It states that the result of running the compiled program is to put the
value of the expression compiled into the accumulator. No registers
except the accumulator and those with addresses ![]() are affected.
are affected.