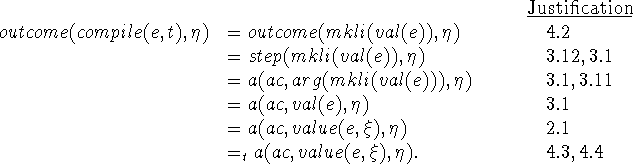
The proof is accomplished by an induction on the expression e being compiled. We prove it first for constants, then for variables, and then for sums on the induction hypothesis that it is true for the summands. Thus there are three cases.
I.isconst(e). We have
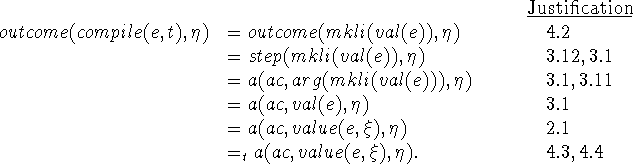
II.isvar(e). We have
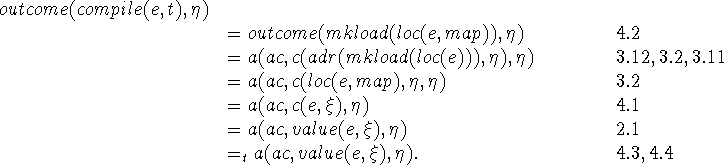
III.issum(e). In this case, we first write
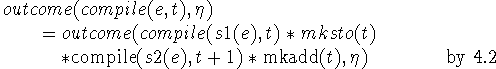
![]()
![]()
using the relation between concatenating programs and composing the functions they represent. Now we introduce some notation. Let
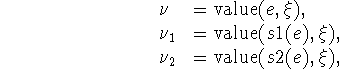
so that ![]() . Further let
. Further let
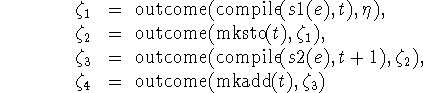
so that ![]() = outcome(compile(
= outcome(compile( ![]() , and we want to prove
that
, and we want to prove
that
![]()
We have
![]()
and
![]()
Now
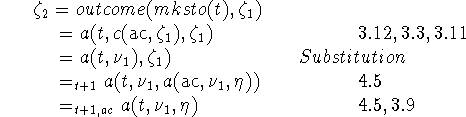
and
![]()
Next
![]()
= ![]()
Here we again use the induction hypothesis that s2(e) is compiled
correctly. In order to apply it, we need
c(loc( ![]() ,map),
,map), ![]() for
each variable
for
each variable ![]() which is proved as follows:
which is proved as follows:

Now we can continue with
![]()
Finally,

This concludes the proof.