Quantified Generalized Logic of Contexts
[
Selene Makarios
The notion of formalized contexts was proposed 8 (8) as a way of addressing the problem of generality in AI. The original idea was to create AI systems that never get ``stuck'' with the set of concepts they are using at any given moment, always being able to transcend any given context to a more general one.
Another perspective is that, for the sake of tractability, contexts allow humans to temporarily fix a domain of discourse and a set of interpretations, for purposes of performing some cognitive or communicative task. Without this ability, that is, if humans were required to always account for all entities, relationships, and the interpretations thereof, while performing a cognitive or communicative task, all such tasks would likely become unmanageable.
McCarthy's and Guha's approach to formalizing context
3 (3); 4 (4); 2 (2) was to introduce an operator `![]() ' , with the
intended intuitive meaning that if
' , with the
intended intuitive meaning that if ![]() is a context, and
is a context, and ![]() is a proposition, then the expression
is a proposition, then the expression
| (1) |
The notion of ``context'' itself is taken as a mathematical primitive in the formalism discussed here. Regardless of what motivating conception of context one employs, what matters is that propositions can be asserted in a context, and then other propositions can be derived in it, or possibly in other contexts that are related to it.
The following are some examples of motivating conceptions of context: a constraint upon time, such as in the Middle Ages, or last Tuesday afternoon; a constraint upon place, such as in the Gobi desert; the context of a given conversation; the context of a particular news report; the context of a fictitious universe, such as the world of Sherlock Holmes; the context of a set of beliefs; a linguistic context, such as a particular tongue, or a collection of application-specific verbal efficiencies1.
As originally described 8 (8); 4 (4), context logic was a relatively informal idea, presented as a syntax with a framework of examples and intuitions, and suggested approaches to applications. Since that time, the goal of providing a complete semantic account of what the language of context logic really says, and what its operations really do - especially for the quantificational case - has proved difficult to achieve.
We believe the present work to be the first offering of a full, rigorous, model-theoretic treatment of quantificational context logic, during the time since context logic was proposed
as a technique in Artificial Intelligence almost twenty years ago. In addition to providing semantics, the formalism described here further generalizes the original concept of ![]() ,
allowing an elaboration where the truth-conditions that determine a system's modalities can themselves be vary with context - in other words, the meaning of
,
allowing an elaboration where the truth-conditions that determine a system's modalities can themselves be vary with context - in other words, the meaning of ![]() itself can be
context-dependent.
itself can be
context-dependent.
The syntax of context logic is not, as is customarily the case with formal languages, defined over the collection of sequences of some set of symbols, though it is generally convenient to project context logic expressions onto paper as arrangements of typographic symbols.
The reason for this decision is that there may exist in one's mind a qualitative distinction between ``terms'' and ``sentences''. First-order logic makes this distinction quite formal. But in context logic, we will need to move smoothly from the idea of propositions whose arguments are merely (what might be called) ``terms'', to propositions having arguments that are (what might be called) ``sentences''.
Thus we avoid the expressions ``symbol'', ``term'', and ``sentence'' altogether. Following the approach proposed by McCarthy 5 (5), define the syntax of context logic in terms of ``abstract syntax-objects'' and ``constructs''. It helps to imagine constructs as data-structures, built up from syntax-objects and other constructs via constructors; the entities that do such building will in fact be called ``constructors''. So, the current sentence is the last place the reader will find the words ``symbol'', ``term'', or ``sentence'' used in this work.
The language ![]() of context logic is defined over a signature
of context logic is defined over a signature
| (2) |
The syntax of context logic employs constructors corresponding to the standard logical connectives ![]() ,
, ![]() , and
, and ![]() (we will liberally use constructors for implication as
well, assuming their analogous definitions in terms of the other constructors); the context-logic specific quantifier-constructors
(we will liberally use constructors for implication as
well, assuming their analogous definitions in terms of the other constructors); the context-logic specific quantifier-constructors
![]() ,
,
![]() ,
,
![]() , and
, and
![]() , for quantifying respectively over contexts, over domain objects, over proposition-objects in
, for quantifying respectively over contexts, over domain objects, over proposition-objects in ![]() itself, and over the objects associated with various contexts (in a way
to be made precise); the existential counterparts
itself, and over the objects associated with various contexts (in a way
to be made precise); the existential counterparts
![]() ,
,
![]() ,
,
![]() , and
, and ![]() of each universal quantifier-construct; and finally, the constructor
of each universal quantifier-construct; and finally, the constructor
![]() .
.
The constructor ![]() is the `
is the `![]() ' constructor, which is a two-place constructor over
' constructor, which is a two-place constructor over
![]() . Intuitively, the construct
. Intuitively, the construct
| (3) |
The set of predicate-objects ![]() optionally includes
optionally includes ![]() . This inclusion corresponds to the case where
. This inclusion corresponds to the case where ![]() is allowed to nest, that is, where the truth of some
proposition asserted relative to a context is itself asserted relative to some context. The function-objects in
is allowed to nest, that is, where the truth of some
proposition asserted relative to a context is itself asserted relative to some context. The function-objects in ![]() may only apply to term-objects, which are either domain-objects in
may only apply to term-objects, which are either domain-objects in
![]() , or are the result of applying function-objects in
, or are the result of applying function-objects in ![]() to term-objects. The predicate-objects in
to term-objects. The predicate-objects in ![]() , except for
, except for ![]() if it is included, may likewise only apply to
term-objects.
if it is included, may likewise only apply to
term-objects.
For brevity, we may resort to using the expressions ``term'', ``function'', ``predicate'', and ``object'' as abbreviations for ``term-object'', ``function-object'', ``predicate-object'', and ``domain-object'', respectively, with the understanding the use of these expressions is simply a convenience with no ontological significance.
The language ![]() has
two
kinds of ``atomic'' constructs,
has
two
kinds of ``atomic'' constructs,
| (4) |
| (5) |
| (10) |
Our notion of a semantic structure is an extension of the classical notion of a semantic structure for first-order logic. For each ![]() in
in ![]() , our context logic structure
, our context logic structure ![]() assigns a context object
assigns a context object
![]() , a function
, a function
![]() to each
to each ![]() in
in ![]() , a predicate
, a predicate
![]() to each
to each ![]() in
in ![]() , and a domain object
, and a domain object
![]() to each
to each ![]() in
in ![]() .
The structure
.
The structure ![]() will also assign a semantic proposition-object
will also assign a semantic proposition-object
![]() to each
to each ![]() in
in ![]() , as will be discussed in more detail later.
, as will be discussed in more detail later.
Thus all ![]() in
in ![]() are rigid designators with respect to context-relative interpretation, but this turns out not to matter. The reason is that there is more to the semantics of
contexts than the particular objects they designate, which turn out to be irrelevant (and could just as well been made non-rigid, writing
are rigid designators with respect to context-relative interpretation, but this turns out not to matter. The reason is that there is more to the semantics of
contexts than the particular objects they designate, which turn out to be irrelevant (and could just as well been made non-rigid, writing
![]() , with notational cost and no
semantic gain). The only characteristic of
, with notational cost and no
semantic gain). The only characteristic of
![]() that has semantic significance, is in fact context-relative, see definition (20). Meanwhile, no syntax objects in
that has semantic significance, is in fact context-relative, see definition (20). Meanwhile, no syntax objects in
![]() ,
, ![]() , or
, or ![]() need be rigid, nor, as it turns out, do the syntax objects in
need be rigid, nor, as it turns out, do the syntax objects in ![]() .
.
The expression ![]() stands for the collection of all
stands for the collection of all
![]() ,
,
![]() stands for all
stands for all
![]() ,
,
![]() stands for all
stands for all
![]() , and
, and
![]() stands for all
stands for all
![]() .
Furthermore,
.
Furthermore,
![]() is the union of all
is the union of all
![]() ,
,
![]() is the union of all
is the union of all
![]() , and
, and
![]() is the union of all
is the union of all
![]() .
.
The semantics of the logical connectives based on a classical first-order structure are in effect for each ![]() . If
. If ![]() is in
is in ![]() , we write
, we write
| (11) |
| (12) |
| (13) |
| (14) |
| (15) |
| (16) |
With ![]() denoting
denoting ![]() occurring free in
occurring free in ![]() , and
, and ![]() denoting
denoting ![]() with
with ![]() replacing
replacing ![]() , we define
, we define
| (17) |
| (18) |
![\begin{displaymath}
\begin{array}{c}
\Miff
{\Ent{{\cS }{c}}{}{\forall_{{c_1}}{a...
...}
{\Ent{{\cS }{c}}{}{\phi[{b}_{}/a]}
}
}
\end{array}\period
\end{displaymath}](img80.png) |
(19) |
The structure ![]() includes a set of possible worlds
includes a set of possible worlds ![]() (intended as the same abstract notion of possible worlds as used in modal logic semantics) and a ``consistency relation''
(intended as the same abstract notion of possible worlds as used in modal logic semantics) and a ``consistency relation''
![]() , where
, where
Intuitively, the expression
| (21) |
As an example of a context logic model, let contexts correspond to closed intervals of real time, and then the possible worlds consistent with a given context ![]() could be given as
those worlds wherein the time falls within
could be given as
those worlds wherein the time falls within ![]() . As another example, if we take contexts to be the logical closures
. As another example, if we take contexts to be the logical closures ![]() of assertions
of assertions ![]() about an arrangement of
objects on a table, then the possible worlds consistent with
about an arrangement of
objects on a table, then the possible worlds consistent with ![]() could be given as those worlds wherein
could be given as those worlds wherein ![]() is satisfied, but where other aspects of the arrangement might
vary.
is satisfied, but where other aspects of the arrangement might
vary.
To say that truth is context-relative is meaningless without some way of comparing truths. One could devise an absolute framework within which relative truth is to be assessed; this
is the case with the modal valuation function ![]() , which is a universal entity governing all world-relative truth.
, which is a universal entity governing all world-relative truth.
But we shall not do this, and instead we leave it to each context to define its own framework within which to assess relative truth. For, ``who'' else is there to assess it? We are declining to require an absolute arbiter of either truth or relative truth, and yet there is no a priori reason to distinguish any one among the contexts themselves for this purpose. The result, of course, is that the assessment of relative truth is itself relative, with each context not only having its own account of what is true, but also a view on what truth means for each among the collection of contexts. Thus, every context can be an arbiter of relative truth, each in its own relative way.
So, for each ![]() , the structure
, the structure ![]() assigns an object
assigns an object
![]() , which is a set
, which is a set
| (22) |
For each ![]() , the structure
, the structure ![]() assigns an object
assigns an object
![]() , which is a set
, which is a set
| (23) |
The semantics of context logic employ self-interpreting structures, that is, ones where the semantic objects in the range of the structure ![]() will themselves have
interpretations assigned to them by
will themselves have
interpretations assigned to them by ![]() . This will prove useful in handling arbitrarily nested
. This will prove useful in handling arbitrarily nested ![]() s (among other things), by offering a kind of internal self-reference at the
semantic level, rather than a language that is expressive enough to represent its own syntax and allow the construction of self-referential sentences.
s (among other things), by offering a kind of internal self-reference at the
semantic level, rather than a language that is expressive enough to represent its own syntax and allow the construction of self-referential sentences.
Moreover, we are not aware of any a priori reason to rule out the idea of self-interpreting semantic structures. Our model-theoretic structures have both domains and ranges
consisting of abstract objects, so it's not difficult to imagine the domain subsuming the range, resulting in self-interpretation. If interpretation under ![]() is idempotent, the
resulting structure will likely be simpler, but this is not a requirement of the model theory.
is idempotent, the
resulting structure will likely be simpler, but this is not a requirement of the model theory.
For each context ![]() , the structure
, the structure ![]() assigns to each atomic construct
assigns to each atomic construct
| (25) |
| (26) |
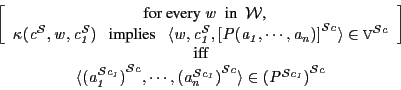 |
(27) |
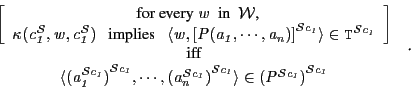 |
(28) |
If ![]() is a first-order atomic construct like (24), then we define, for each
is a first-order atomic construct like (24), then we define, for each ![]() in
in ![]() ,
,
If ![]() includes
includes ![]() , so that
, so that ![]() can nest, we address the issue of defining
can nest, we address the issue of defining
| (41) |
| (43) |
| (44) |
This completes the semantics for nested ![]() s. Note that further nesting of
s. Note that further nesting of ![]() does not compound matters further - the self-interpreting structure
does not compound matters further - the self-interpreting structure ![]() provides interpretation
for arbitrary nesting depths.
provides interpretation
for arbitrary nesting depths.
One intuitively desirable property of contexts is that two propositions each hold separately in a context if and only if their conjunction holds there as well
9 (9); 1 (1); 2 (2); 7 (7). Requiring more, such as the disjunctive analog, would not be in accordance with
certain intuitive conceptions of context that humans may use. For example, using time intervals as contexts as mentioned earlier, while it should be the case that
| (45) |
| (46) |
As it turns out, for the conjunctive version of this property, the choice is made for us, as the conjunctive condition always holds.
Note that this is not the analog of the Barcan formula and its converse. The treatment of the Barcan analogs involves analogs of the necessary and possible operators, described in terms of the collection of contexts, and will be addressed in a future work.
| (49) |
| (50) |
| (51) |
| (52) |
As a result of the two previous theorems in this section, we have, for ![]() ,
,
This turns out to be a feature, not a bug, because, for example, in a context logic language ![]() where
where ![]() does happen to distribute over disjunction, the analogous result would be
does happen to distribute over disjunction, the analogous result would be
![]()
![]()
![]() for
for ![]() . If setting
. If setting ![]() to
to ![]() were an option in this case (which it
obviously isn't), then we would then require that always
were an option in this case (which it
obviously isn't), then we would then require that always
![]() .
.
And while that might initially might seem a natural-enough looking thing, it is in fact completely counter-intuitive, for it requires, for such a language, that if a contradiction
arises in some context - let us take the particular context in which Fred is in both Denmark and New Zealand at the same time - then a contradiction must exist outside of that
context. Thus, by not insisting that the ![]() -way combination in (70) holds for
-way combination in (70) holds for ![]() , the machinery of context logic appears to be intrinsically protecting the integrity
of the intuitive notion of context.
, the machinery of context logic appears to be intrinsically protecting the integrity
of the intuitive notion of context.
| (54) |
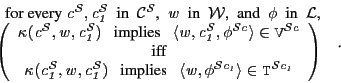 |
(55) |
![\begin{displaymath}
\MforallThreeln
{{\cC}^{\cS }}
{{{c}^{\cS }_{}},{{c}^{\cS ...
..._{}^{{\cS }{{c}_{2}}}}}
}
}
}
\right)}
\right]}
}
\period
\end{displaymath}](img151.png) |
(56) |
| (57) |
We add the constructor
![]() to those of the language
to those of the language ![]() . If
. If ![]() and
and ![]() are in
are in ![]() and
and ![]() is in
is in ![]() , then
, then
| (58) |
For each ![]() , the structure assigns at
, the structure assigns at ![]() an object
an object
![]() , which is a set
, which is a set
| (60) |
| (61) |
Semantically, we define
![\begin{displaymath}
\Mifflnln
{\Ent{{\cS }{c}}{}{\Ist{c_2}{c_1}{\phi}}
}
{\Mf...
...exttt{T}}_{c_2}^{{\cS }{{c}_{1}}}}}
}
}}
\right]}
}
\period
\end{displaymath}](img161.png) |
(62) |
![\begin{displaymath}
\Mifflnln
{\Ent{{\cS }{c}}{}{\Ist{}{c_2}{\Ist{}{c_1}{\phi}}...
...exttt{T}}_{}^{{\cS }{{c}_{2}}}}}
}
}
\right)}
\right]}
}
}
\end{displaymath}](img164.png) |
(63) |
By definition,
| (64) |
| (65) |
[Still need to add Guha's work...]
Also related is Buvac's 10 (10) treatment of the semantics of propositional context logic. Interestingly, we find in that work, something like a propositional precursor of the concept of the consistency relation:
``Naively, a context is modelled by a set of truth assignments, that describe the possible states of affairs of that context. Thus a model will associate a set of truth assignments with every context. These truth assignments reflect the state of affairs which are possible in a context. For a proposition to be true in a context it has to be satisfied by all the truth assignments associated with that context.''
We can identify truth assignments with possible worlds, and note that a set of these is associated with each context. The concept of the consistency relation ![]() , of course,
does not assume that possible worlds are truth-assignments - any notion of possible world is admitted as the worlds are abstract. However, the choice of truth-assignments was of
course the only available one in the case of propositional logic, since there are no terms available by which possible worlds could be parameterized.
, of course,
does not assume that possible worlds are truth-assignments - any notion of possible world is admitted as the worlds are abstract. However, the choice of truth-assignments was of
course the only available one in the case of propositional logic, since there are no terms available by which possible worlds could be parameterized.
[Rolf Nossum stuff]
[...] the work of the Trento group, in particular the work of Chiara Ghidini on distributed first-order logics, which offers a kind of semantics for contexts. We note the following properties of their semantic approach.
LMS appears to assume that all contexts agree on what ``possible situations'' comprise each context. Thus, the contexts are required to be independent of context. This is a restriction that McCarthy, the author of the seminal work on contexts, has specifically said 7 (7) he would not choose to impose. This is an optional constraint (``homogeneity'') in the semantics presented here, and upon which our model-theoretic machinery does not rely.
LMS appears to assume that all contexts agree on what propositions hold in what contexts. Note of course that the contexts are free to make conflicting claims about propositions, but they are all still required to be in agreement on who claims what. This is another optional constraint (``coherence'') upon which our model-theoretic machinery does not rely.
LMS appears to assume that where the set of ``possible situations'' of two given contexts overlap, the contexts agree on the values of propositions in that overlap - in fact, this assumption seems to be built-in to the very relations that define ``context''. Again we treat this is an optional constraint (``consensus'').
LMS appears to assume an at-most countable, extensionally-defined, collection of contexts. This is a reasonable approach for tasks such as treating a distributed team of N autonomous agents, which seems to be an important type of motivating example for their work, but is not applicable to modelling any notion of context defined over continuous sets. The approach defined in the current work can use any set of contexts, extensional or intensional, of any cardinality.
In LMS a single set of truth conditions governs all the contexts, thereby in effect requiring a context-independent notion of ![]() . Again this is an optional constraint in our
semantics.
. Again this is an optional constraint in our
semantics.
We have not been able to identify something corresponding to the nesting of ![]() in LMS, or to quantification over propositions.
in LMS, or to quantification over propositions.
[need citations]
[yada]
10 Comparison with other logics of context The propositional logic of ist(c; Ã) is investigated in (Buva.c et al. 1995), and augmented with first-order quantification in (Buva.c 1996). These are axiomatic systems for reasoning with ist-formulas asserted in given contexts. The syntax for asserting Á in context c is c : Á, and a central motivation for these logics is the ability to enter a given context, perform some reasoning there according to facts that hold in that context, and exit with the results so obtained. In general, this gives rise 16 to a stack c of contexts having been entered into and not exited from, and these are the deduction rules governing entry into and exit from contexts: Enter: ` c : ist(c; Ã) ` cc : à Exit: ` cc : à ` c : ist(c; Ã) The Enter rule is not listed in the axiomatic presentation of (Buva.c et al. 1995), and it is subsumed by other axioms and rules of the logic. It is included here for symmetry. The semantics of (Buva.c 1996) does not distinguish between ist(c; ist(d; Á)) and ist(d; Á), which appears anomalous at first blush. The rules for entering and exiting contexts are correspondingly constrained: Enter: ` x : ist(c; Ã) ` c : à Exit: ` c : à ` x : ist(c; Ã) The logic remembers only the last context that has been entered into. This phenomenon, called flatness, is not unavoidable however, and as discussed below, (Nossum 2002) generalizes the propositional logic of ist(c; Á) to an algebraically generated spectrum of context logics where flat contexts are only a special case. We may compare our Á¡± à with 8c : ist(c; Á ! Ã) of (Buva.c 1996). The latter formula can be taken as rephrasing our semantical clause for the former. If the two are accepted as variants of each other, then Buva.c’s system is seen to be strictly more expressive than the one presented here, because it has full first-order quantification, over context variables as well as other variables. But as usual expressivity comes at a price: the system of (Buva.c 1996) is not decidable. To further illuminate the trade-o® that a®orded us decidability in the present logic, let us point out our axiom A2, which may be taken to express that each individual context is a logically coherent and complete entity. That is a stricter assumption than in most other logics of context, including other logics studied by this author (Nossum 2002), (Nossum and Serafini 2002), (Gabbay and Nossum 2000). 17 van Benthem (van Benthem 1996) finds that the term ’context’ denotes a convenient methodological fiction, rather than a well-defined ontological category. His proposal is for an indexing scheme, where each language element can be decorated with an index specifying an intended context for evaluation. This results in a logic where transition between contexts has a natural expression. Giunchiglia, Serafini et.al. have also developed logical systems of context where transition between contexts is the main concern (Serafini and Giunchiglia 2001). Each context is modelled by a separate natural deductive system, and there are special rules for inter-context deduction. However, there is no direct provision for nesting of contexts, as in ist(c; ist(d; Á)), although the natural deduction system allows for convenient passage between c and d. Nossum and Serafini have developed natural-deductive systems of context where context combination is catered for through an algebraic component (Nossum and Serafini 2002). Sequential composition of contexts, e.g. c; d; e; : : :, is represented associatively by algebraic terms, e.g. c © d © e : : :, and there is provision for algebraic equations on context terms, thus spanning a variety of natural-deductive logics of context including flat contexts, context sets, context multisets, and context sequences. (Nossum 2002) expands on the idea of algebraic context augmentation in the framework of an axiomatic ist-logic in the style of (Buva.c et al. 1995). This time, context terms like c©d©e are introduced into the syntax of the language, as are algebraic equations on ground context terms. The equational varieties within the scope of this approach are the same as in (Nossum and Serafini 2002), including flat contexts, context sets, context multisets, and context sequences. Augmenting a context w with another one, c, to form a composite context w © c, is analogous to going from possible world w to possible world w?c in the logic of the present paper. Ongoing work aims to generalize (Nossum 2002) to wider equational varieties and quasi-varieties, as well as to quantificational logic. In (Gabbay and Nossum 2000) a quantificational system similar to Buva.c’s is obtained by self fibring of predicate logics, and decidability is shown in a special case. They also develop a multi-modal logic for ist(Á; Ã), which is as expressive as the present logic for Á¡± Ã, but they do not prove decidability for it. 18 11 Conclusion We depart from the notation ist(c; Ã) which originates with (Guha 1991), preferring c¡± à and generalizing to Á¡± Ã. Our system harnesses generalization over contexts in a two-layered multi-modal system, the semantics of one modality quantifying over a set of simpler modalities. This results in a simple, decidable, sound, and complete axiomatic presentation.
Just as modal logic was inspired by the desire to model certain aspects of human cognition and communication richer than those expressible in first-order logic, such as the use of tenses and propositional attitudes, context logic was offered to model perhaps deeper aspects of human cognition and communication which may be key to obtaining human-level AI. We hope that this formal model theory for context logic will be of use in working toward that goal.
This document was generated using the LaTeX2HTML translator Version 2002-2 (1.70)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html context-semantics
The translation was initiated by selene on 2005-06-02