In this section and the next, we show how
the ideas outlined above can be applied to
formalize and reason about heuristics for
moving blocks in order to solve planning
problems in the blocks world. The strategies
formalized in the paper describe different
algorithms for solving planning problems in
the elementary blocks world domain [Gupta & Nau1991].
First, we summarize a very elegant and simple
formalization of STRIPS in the situation
calculus, and its application to reasoning
about action in the blocks world, described
in [McCarthy1985]. Then, we propose a
nested abnormality theory (NAT)
[Lifschitz1995]
that solves the problem of projecting the
strategy described by axioms 
to
. In section 3, this theory
is generalized into a class of NAT's
which apply circumscription in a particular way
that is useful for studying the projections of
declarative formalizations of strategies of the
sort described in this paper.
In [McCarthy1985], John McCarthy proposes a very simple formalization of STRIPS [Fikes & Nilsson1971] in the situation calculus. The formalization is as follows. STRIPS is a planning system that uses a database of logical formulas to represent information about a state. Each action has a precondition, an add list, and a delete list. When an action is considered, it is first determined whether its precondition is satisfied. If the precondition is met, then the sentences on the delete list are deleted from the database, and the sentences on the add list are added to it.
There are variables of the following sorts:
for situations (s,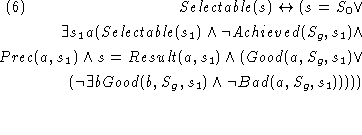 
, ...), for
actions (a, 
, ...), and for
propositional fluents (p, 
, ...
)
.
Associated with each situation is a database
of propositions, and this gives us the wff
DB(p,s) asserting that p is in
the database associated with s. The
function Result maps a situation s
and an action a into the situation that
results when action a is performed in
situation s.
STRIPS is characterized by three predicates: (1) Prec(a,s) is true provided action a can be performed in situation s; (2) Delete(p,a,s) is true if proposition p is to be deleted when action a is performed in situation s; (3) Add(p,a,s) is true if proposition p is to be added when action a is performed in situation s. STRIPS has the single axiom
In [McCarthy1985], an example of how to
use this formalization of STRIPS to reason
about action in the blocks world is given.
The example is as follows (we have modified
the initial conditions, and added a
uniqueness of names axiom). The variables
x, y and z range over
blocks. The constant blocks used in the
example are A, B, C, D, E, F, and
T (for Table). The one kind
of propositional fluent is
On(x,y) describing the fact that
block x is on block y.
The one kind of action
is Move(x,y) denoting the act of
moving block x on top of block y.
We assume uniqueness of names for every
function symbol, and every pair of distinct
function symbols. The initial situation
is described by axiom .
The precondition, delete and add
lists of Move(x,y) are characterized
by axioms ,
and , respectively.
For example, from axioms to
we can prove that
In order to interpret action selection rules,
such as axioms to ,
in terms of the theory of action described above,
we need to establish a connection between what
holds at a situation and what is in the
database associated with that situation.
The databases in the formalization of the
blocks world presented above contain only
propositional fluents of the form On(x,y)
for x, y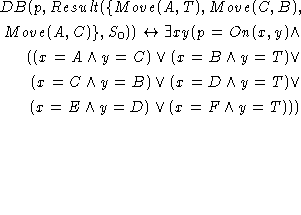 
{A,B,C,D,E,F,T}. These
propositional fluents are called frame
fluents [McCarthy & Hayes1969] [Lifschitz1990],
since any configuration of the blocks
A,B,C,D,E, and F can be
described by combinations of their
values.
The following axiom states that a frame fluent holds at a particular situation if and only if it is in the database associated with that situation.
The expression 
means that 
can be reached [Reiter1993] from s
by executing a nonempty sequence of actions
( 
is an abbreviation for
) .
We include domain closure axioms for blocks,
actions and situations. Axiom
restricts the domain of situations to those
that can be reached from the initial situation
or from the goal situation 
.
Finally, we introduce an axiom of induction
for situations , which allows
us to prove that a property holds for all the
situations that can be reached from a given
situation.
In addition to frame fluents, we use a
number of derived fluents, such as
clear, final, above, tower-deadlock,
terminal, and achieved, which are
partially
defined in terms of the frame fluents.
Axiom describes the configuration
of the goal situation 
.
In general, a problem will be described by
a set of conditions on some initial and goal
situations. The particular problem described
by axioms and
characterizes completely the state of the
initial and goal situations, but this needs
not be the case. Specifying a set of
constrains on initial and goal situations
allows defining classes of problems, instead
of particular instances. Such constraints can
be used then to reason about the behavior of
different strategies on a class of problems.
The formulas presented so far allow us to
prove that some actions are good, bad
or better than others for a given goal
and a particular situation. But we aren't
still able to decide which situations are
selectable according to a particular
strategy.
Action selection rules do not give us
complete information. They don't tell us
which actions are ``not good'', ``not bad'',
or ``not better'' than others. In order to
interpret them in terms of action selection
(using axiom ),
we need to be able to jump to the conclusion
that an action is ''not good'' or ``not bad''
unless the heuristics known so far (axioms
to ) imply
that it is so. This incompleteness
of our formalization is also one of its main
advantages, because it allows us to refine
the problem solving strategy of a program by
simple additions of better heuristics.
We illustrate this idea with an advice
taking scenario later on.
The nested abnormality theory described
below characterizes the behavior of the
strategy described by axioms to
when it is applied to solve the
problem described by axioms
and . That is, it allows us to
determine what situations (and, therefore,
what sequences of actions) can be selected
according to the strategy.
Let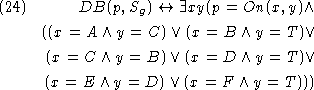 
be the conjunction of the
universal closures of the formulas
to .
The expression describes a
nested abnormality theory in which
circumscription is
applied in the following way. The predicate
Good is circumscribed with respect to
the universal closures of the axioms describing
the strategy of the program (axioms
to ). The predicate
Bad is circumscribed with respect to
the result of the circumscription described
above and the universal closure of axiom
, which contributes to the
definition of Bad with positive
instances of
Better. We need to let Better
vary, because minimizing the extension of
Bad may affect (through axiom
) the extension of
Better. The latter circumscription,
which characterizes the extensions of the
predicates Good and Bad, is
conjoined with 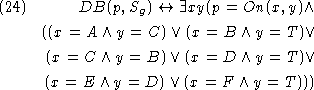, which describes the
theory of action assumed for the blocks world
(axioms to ), the
specific problem reasoned about (axioms
and ), and the
mechanism for action selection (axiom
).
