The characterization of the semantics of
NAT's in terms of second order logic
theories including circumscription formulas
and proposition 1 in [Lifschitz1995]
allow us to prove the equivalence between
the following axiom sets
.
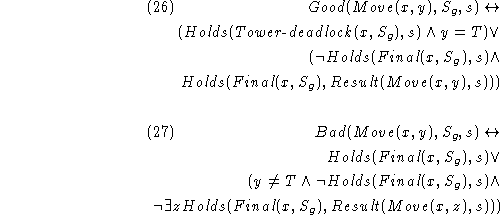
Now, we use several rules for computing circumscription described in [Lifschitz1993]. The first equivalence below can be proved using formula (19) and proposition 2 in [Lifschitz1993]. The second equivalence uses formula (19) and proposition 3 in that paper.
Using the equivalence (27) in
section 3.2 of [Lifschitz1993], we can
prove that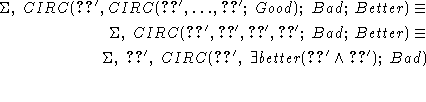 
is
equivalent to the following formula, which
does not depend on better.
Finally, predicate completion [Lifschitz1993] give us the result of the theorem.
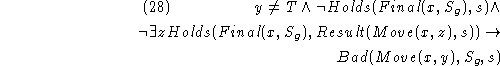
Theorem 1 shows that the nested abnormality
theory described by 
is
equivalent to the second order theory
whose axioms are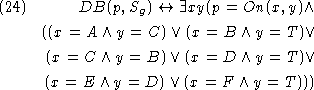 
, and
. This means that using theorem
proving methods for first order
logic we can
decide the selectability of any situation
with respect to the strategy described by
axioms to . For
example, we can prove that action
Move(A,T) is selectable at 
(i.e.,
),
but action Move(C,T) is not (i.e.,
).
