The nested abnormality theory described by
not only solves the problem
of projecting a specific strategy, it
also describes a particular use of
circumscription that allows reasoning
about declarative formalizations of
strategies of the sort proposed in this
paper. The expression
(strategy) denotes the
nested abnormality theory described by
parameterized for different
strategy descriptions
. The idea
is to replace axioms to
by other sets of axioms describing different
strategies, so that we can reason about the
behavior of different strategies.
We describe a scenario in which a program uses
(strategy) to reason about
declarative formalizations of strategies.
The program starts with an empty strategy.
As different heuristics are suggested by
the adviser, the program considers how
they may affect its problem solving
behavior, and reacts accordingly.
The scenario tries to illustrate the idea that a program capable of reasoning non-monotonically about declarative formalizations of strategies can have interesting reflective behavior [McCarthy1990b] [McCarthy1995] [Steels1996] [Sierra1996]. For example, it can save computational resources by detecting uncomputable or incorrect strategies. It can determine which of the heuristics is told improve, are redundant, partially redundant, or inconsistent with its current strategy. It can improve its problem solving strategy, accordingly, by adding and substituting action selection rules and axioms. It can avoid inconsistencies, which may cause it to have an arbitrary behavior. It can learn by taking advice [McCarthy1959], and reflecting on it.
Figure: Behavior of different strategies
for solving planning problems in the blocks
world: (1)
Strategy-1 and Strategy-3 are
both uncomputable, since they allow cyclic
behaviors;
(2) Strategy-2 describes a computable
but incorrect strategy, its unique terminal
situation is not a solution;
(3) Strategy-4 and Strategy-5
describe two computable and correct
strategies, together with their projections
for a particular blocks world problem. It can
be easily observed that Strategy-5 is
better than Strategy-4.
Initially, the advisor suggests to use
the following heuristic:
If a block can be moved to final
position, this should be done right away.
The program constructs Strategy-1,
which is described by axiom .
The projection of Strategy-1 allows
cyclic behaviors, such as the one described
in fig. . The program
concludes that Strategy-1 is not
computable.
We use the following formula to identify
cycles in the projections of
state-based strategies.
The expression 
means that
there is a nonempty
sequence of selectable
situations that leads from s to 
.
A state-based strategy contains a
cycle (axiom ) if there
is a nonempty sequence of selectable situations
that leads from a situation s to a different
situation with the same associated state
(i.e., whose associated database contains the same
formulas as the database associated with s).
In particular, the program can prove that
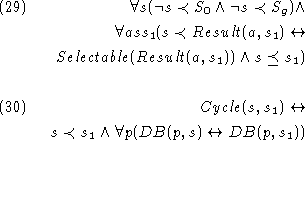holds
in the projection of Strategy-1 by
finding appropriate values for s and
.
The program asks for more advice, instead of
trying to apply Strategy-1 to solve
the problem. The advisor proposes a
different heuristic:
If a block is not in final
position and cannot be moved to final
position, it is better to move it to the
table than anywhere else.
The program constructs Strategy-2,
which is described by axiom
.
The projection of Strategy-2 is shown
in fig. . Strategy-2 is
an incorrect strategy, because
it allows terminal situations which do not
satisfy the goal conditions.
The program still needs more advice. The
advisor suggests now to consider both
heuristics together.
The program constructs Strategy-3,
which is described by axioms
and .
The projection of Strategy-3 still
allows cyclic behaviors, such as the one
described in fig. ,
i.e. it satisfies
.
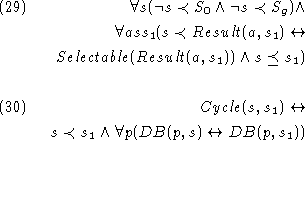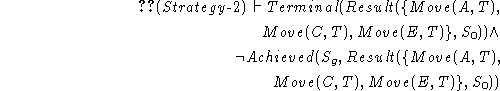
The advisor suggests a third heuristic:
If a block is in final position, do not move
it. The program constructs Strategy-4
as the set of axioms to .
The set of situations that are selectable
according to projection of Strategy-4
(see fig. ) is finite.
The program knows the strategy is correct,
since all its terminal situations happen to be
solutions. The second order axiom of induction
for situations () is needed here
in order to prove that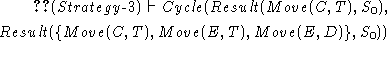 
holds
for all the situations not mentioned in the
theorem below.
The advisor suggests a fourth heuristic:
If there is a block that is above a block it
ought to be above in the goal configuration
but it is not in final position
(tower-deadlock), put it on the table.
The program constructs Strategy-5
as the set of axioms to
. The set of situations that
are selectable according to projection of
Strategy-5
(see fig. ) is finite.
The program can prove that Strategy-5 is
correct. It can also conclude that
Strategy-5 is better than Strategy-4,
since it always solves the problem performing a
smaller or equal number of actions.
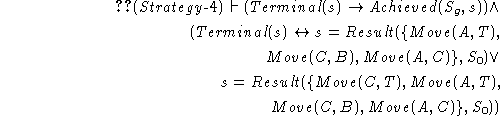
The advisor still suggests a fifth heuristic: If a block is on the table but not in final position, do not move anything on that block.
The program constructs Strategy-6
as the set of axioms
to and . It can
check that the projections of
Strategy-5 and Strategy-6 are
identical. This means that suggestion
is redundant with its
current strategy. Therefore, including
it in the database will not improve the
program's behavior.
The advisor finally suggests a sixth heuristic: If there is a block that is above a block it ought to be above in the goal configuration but it is not in final position (tower-deadlock), it is better to move it on top of a clear block that is in final position and should be clear on the goal configuration than anywhere else.
We use the following formula to detect
inconsistencies in the projection
of a strategy. The formulas
,
and are examples of
verification axioms that can be added
to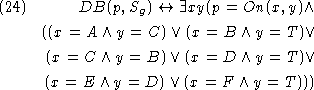 
in order to reason about the
behavior of different strategies.
The program constructs Strategy-7
as the set of axioms
to and .
Although axiom describes
a plausible heuristic, it is in contradiction
with axiom . For example, axiom
implies that Move(A,T) is
good in the initial situation, whereas axioms
and imply
that Move(A,T) is bad.
Using axiom , the program
can prove that Strategy-7 is
inconsistent.
Therefore, it rejects suggestion ,
because it is inconsistent with its current
strategy.
